(Note that we write compositions from left to right and accordingly apply most maps on the right.)
Def.1
A functor ![]() is called a left adjoint to a functor
is called a left adjoint to a functor ![]() if there is a bijection between the homsets:
if there is a bijection between the homsets:
![]()
natural in both ![]() and
and ![]() . In this case
. In this case ![]() is called a right adjoint to
is called a right adjoint to ![]() , and we write
, and we write ![]() .
.
Def.2
A functor ![]() is called a left adjoint to a functor
is called a left adjoint to a functor ![]() if there are natural transformations
if there are natural transformations ![]() and
and ![]() satisfying the zig-zag identities:
satisfying the zig-zag identities:
![]()
So, why are these two definitions equivalent?
We start out from Def.2, as it generalizes to arbitrary bicategory or double category, which enable morphisms (‘transformations‘ or ‘2-cells‘) between [parallel] arrows. Transformations will be depicted by a dashed arrow symbol: ![]() .
.
We are using the bicategory ![]() which has functors as arrows and natural transformations as transformations, and the bicategory
which has functors as arrows and natural transformations as transformations, and the bicategory ![]() which has profunctors as arrows. And we are going to pass them both to Ehresmann’s double category construction of ‘quintets‘.
which has profunctors as arrows. And we are going to pass them both to Ehresmann’s double category construction of ‘quintets‘.
In short, we will obtain a full inclusion of (doubly weak) double categories of the quintets of ![]() into that of
into that of ![]() which is covariant for vertical arrows but contravariant for horizontal arrows, hence taking adjunctions to companions and companions to adjunctions.
which is covariant for vertical arrows but contravariant for horizontal arrows, hence taking adjunctions to companions and companions to adjunctions.
Noting that companions are just ismorphisms in the ambient bicategory, we will conclude that an adjunction in ![]() corresponds to an isomorphism in
corresponds to an isomorphism in ![]() and a natural isomomorphism (in particular, the identity of any functor) in
and a natural isomomorphism (in particular, the identity of any functor) in ![]() corresponds to an adjunction in
corresponds to an adjunction in ![]() .
.
Note that, both sides of the natural bijection in Def.1 are functors ![]() , i.e. are profunctors.
, i.e. are profunctors.
Specifically, they above are denoted by ![]() and
and ![]() , that is, for a single functor
, that is, for a single functor ![]() , we define
, we define
![]()
In the terminology of heteromorphisms, we can get ![]() if we take a copy from each arrow in
if we take a copy from each arrow in ![]() of the form
of the form ![]() and regard them as heteromorphisms
and regard them as heteromorphisms ![]() . The copy of
. The copy of ![]() is a reflection arrow
is a reflection arrow ![]() (into the full subcategory
(into the full subcategory ![]() ), these generate the profunctor
), these generate the profunctor ![]() .
.
Similarly, ![]() is generated by the coreflection arrows
is generated by the coreflection arrows ![]() .
.
Importantly, it turns out that there is an adjunction ![]() in the bicategory
in the bicategory ![]() of categories and profunctors, for any functor
of categories and profunctors, for any functor ![]() (according to Def.2).
(according to Def.2).
In the setting of bicategories [double categories], one can already prove uniqueness of left/right adjoint for a given arrow (up to isomorphism) and the following interchanging rules, which assert one-to-one correspondences between the transformations below, supposed ![]() :
:
![]()
The mappings ![]() and
and ![]() extend to two natural embeddings of the bicategory
extend to two natural embeddings of the bicategory ![]() , whose arrows are the functors, into
, whose arrows are the functors, into ![]() .
.
Note that ![]() is contravariant on arrows (reverses source/target and composition of functors) while
is contravariant on arrows (reverses source/target and composition of functors) while ![]() is contravariant on the natural transformations.
is contravariant on the natural transformations.
To express these as covariant mappings, the notations ![]() and
and ![]() are introduced for the bicategory obtained from
are introduced for the bicategory obtained from ![]() by reversing arrows / transformations, respectively.
by reversing arrows / transformations, respectively.
Using the interchange rules, we show below how to arrive to the embedding ![]() when starting out from
when starting out from ![]() , touching an embedding of double categories,
, touching an embedding of double categories, ![]() , in the middle of the way:
, in the middle of the way:
A diagram of functors 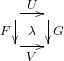 with
with ![]() induces and is determined by any of the following profunctor morphisms:
induces and is determined by any of the following profunctor morphisms:
![Rendered by QuickLaTeX.com \[\EEE{\lambda^*:\,G^*U^*\tto V^*F^*}{U^*\tto G_*V^*F^*}{\begin{matrix}\\ \phantom{_} \lambda^J:\,U^*F_*\tto G_*V^*\\ \phantom{_} \end{matrix}}{F_*\tto U_*G_*V^*}{\lambda_*:\,F_*V_*\tto U_*G_*}\]](https://profunctors.zellerede.tk/wp-content/ql-cache/quicklatex.com-789d3e270139f9df210ec897c46b9648_l3.png)
In a double category, transformations ![]() are supported by a pair of ‘vertical arrows‘ (regarding the original arrows as horizontal ones), and thus are depicted and also called as squares (or ‘cells’).
are supported by a pair of ‘vertical arrows‘ (regarding the original arrows as horizontal ones), and thus are depicted and also called as squares (or ‘cells’).
Horizontally adjacent squares, as well as horizontal arrows can be associatively composed horizontally, with units.
Vertically adjacent squares, as well as vertical arrows can be associatively composed vertically, with units.
The so called Ehresmann double category ![]() can be defined
can be defined![]() for any bicategory
for any bicategory ![]() : all the arrows of
: all the arrows of ![]() are considered both vertical and horizontal in
are considered both vertical and horizontal in ![]() , with squares
, with squares 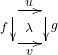 as transformations
as transformations ![]() .
.
Now we are ready to define our embedding ![]() : its source is the double category
: its source is the double category ![]() , and its target is the double category
, and its target is the double category ![]() , and
, and ![]() flips horizontal arrows and horizontal composition.
flips horizontal arrows and horizontal composition.
So that ![]() . All objects (the categories) are fixed, a horizontal arrow (a functor
. All objects (the categories) are fixed, a horizontal arrow (a functor ![]() ) is mapped to
) is mapped to ![]() , while a vertical arrow (a functor
, while a vertical arrow (a functor ![]() ) is mapped to
) is mapped to ![]() and a square
and a square ![]() is mapped to the corresponding square of
is mapped to the corresponding square of ![]() . Compositions just work fine.
. Compositions just work fine.
Explicitly, ![]() sends the pair of generating heteromorphisms
sends the pair of generating heteromorphisms ![]() to the composite
to the composite ![]() for any
for any ![]() .
.
Adjunction ![]() in a double category is interpreted between a vertical
in a double category is interpreted between a vertical ![]() and horizontal
and horizontal ![]() , in such a way that
, in such a way that ![]() in
in ![]() for a bicategory
for a bicategory ![]() translates readily to
translates readily to ![]() being left adjoint to
being left adjoint to ![]() in
in ![]() , according to Def.2.
, according to Def.2.
If we flip horizontal arrows in a double category, adjunctions become companions:
A pair of horizontal and vertical arrows ![]() ,
, ![]() are said to be a companion pair, if there exist squares
are said to be a companion pair, if there exist squares ![]() as below
as below
![Rendered by QuickLaTeX.com \[\nzt{1_A}{1_A}\eta fu\quad\quad \nzt uf\eps{1_B}{1_B}\]](https://profunctors.zellerede.tk/wp-content/ql-cache/quicklatex.com-29980538fa71edef39cc629930264256_l3.png)
such that ![]() and
and ![]() (vertical composition)
(vertical composition) ![]() .
.
It is easy to see, that a companion in ![]() is just a pair of parallel isomorphic arrows in
is just a pair of parallel isomorphic arrows in ![]() .
.
Since ![]() flips horizontal arrows,
flips horizontal arrows, ![]() takes adjunctions to companions and companions to adjunctions.
takes adjunctions to companions and companions to adjunctions.
Moreover, ![]() is surjective on squares.
is surjective on squares.
Put it all together, we get that
two functors are naturally isomorphic ![]() if and only if there is an adjunction of profunctors
if and only if there is an adjunction of profunctors ![]() . (This is basically one of the key observations above that
. (This is basically one of the key observations above that ![]() .)
.)
And, finally,
two functors are adjoint
according to Def.2 if and only if we have an isomorphism of profunctors
, i.e. Def.1 holds.
![]() Remark. Actually, there are issues about formalizing Ehresmann’s construction for general bicategories.
Remark. Actually, there are issues about formalizing Ehresmann’s construction for general bicategories.
When composition of arrows in a bicategory is strictly associative, we indeed get a (still strictly associative) double category ![]() . Otherwise, however, the resulting double category would be only weakly associative both horizontally and vertically, and such animals can only be defined by workarounds, e.g. using higher dimension categories with special collapses.
. Otherwise, however, the resulting double category would be only weakly associative both horizontally and vertically, and such animals can only be defined by workarounds, e.g. using higher dimension categories with special collapses.
But don’t panic, we can still make things precise by introducing adequate maps from double categories to bicategories, so that ![]() would become such a map
would become such a map ![]() , with all its good properties, in particular taking companions to adjunctions and an adjunction to a pair of isomorphic arrows.
, with all its good properties, in particular taking companions to adjunctions and an adjunction to a pair of isomorphic arrows.
