We generalize the following results of infinitary first order logic:
A class ![]() of models is axiomatizable by universal / existential / positive / negative formulas iff it is closed under submodels / extensions / homomorphic images / surjective homomorphic preimages.
of models is axiomatizable by universal / existential / positive / negative formulas iff it is closed under submodels / extensions / homomorphic images / surjective homomorphic preimages.
Assume we are given a class ![]() of ‘models’ and a class
of ‘models’ and a class ![]() of formulas, forming a (complete) Boolean algebra (so that operations ‘and’/’or’ are defined for arbitrary many formulas), and assume we are given a complete Boolean relation
of formulas, forming a (complete) Boolean algebra (so that operations ‘and’/’or’ are defined for arbitrary many formulas), and assume we are given a complete Boolean relation ![]() between them (for ‘validity’), i.e. a relation satisfying
between them (for ‘validity’), i.e. a relation satisfying ![]() and
and ![]() .
.
Let ![]() .
.
We write ![]() and
and![]() .
.
A class of models ![]() is axiomatizable by
is axiomatizable by ![]() -formulas if
-formulas if ![]() for some
for some ![]() , equivalently, if
, equivalently, if ![]() .
.
Let ![]() be a reflexive binary relation on the class of models (typically stating the existence of a morphism of certain type), and write
be a reflexive binary relation on the class of models (typically stating the existence of a morphism of certain type), and write ![]() , similarly define
, similarly define ![]() .
.
Definition. A binary relation ![]() is modelwise expressible by
is modelwise expressible by ![]() -formulas, if for every model
-formulas, if for every model ![]() there is a formula
there is a formula ![]() which is valid on
which is valid on ![]() , and whenever
, and whenever ![]() , it implies
, it implies ![]() .
.
Examples.
Let the formulas be infinitary first order formulas for a similarity type ![]() , and the models be the corresponding relational / algebraic structures.
, and the models be the corresponding relational / algebraic structures.
- Let
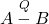 mean that
mean that 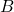 is a homomorphic image of
is a homomorphic image of 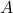 , i.e. isomorphic to a quotient of
, i.e. isomorphic to a quotient of 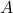 , and choose
, and choose  to be the class of positive formulas. Set
to be the class of positive formulas. Set![Rendered by QuickLaTeX.com \[\delta_A:=\exists (x_a)_{a\in A}:\Delta_0(A)\land\forall y:\bigvee_{a\in A}(y=x_a)\]](https://profunctors.zellerede.tk/wp-content/ql-cache/quicklatex.com-1a67904547d20e00c203ebcfcdb6c040_l3.png)
where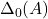 is the conjunction of all atomic predicates that hold in
is the conjunction of all atomic predicates that hold in 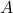 , the element
, the element  replaced by the corresponding variable
replaced by the corresponding variable 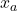 .
. - Let
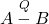 mean that
mean that 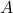 is isomorphic to a substructure of
is isomorphic to a substructure of 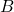 , i.e. there is a relationally full embedding
, i.e. there is a relationally full embedding 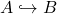 , and choose
, and choose  to be the class of existential formulas. Set
to be the class of existential formulas. Set![Rendered by QuickLaTeX.com \[\delta_A:=\exists (x_a)_{a\in A}:\Delta_0(A)\land\bigwedge_{\sigma:A\not\models\sigma\,[x_a/a]}\lnot\sigma\]](https://profunctors.zellerede.tk/wp-content/ql-cache/quicklatex.com-a71038a26536907d31c8b466c0965e5f_l3.png)
where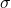 runs over atomic formulas which are not valid on
runs over atomic formulas which are not valid on 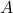 under the substitution
under the substitution 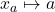 .
.
Theorem. Suppose ![]() is modelwise expressible by
is modelwise expressible by ![]() -formulas. Then
-formulas. Then
a) If ![]() , then
, then ![]() is axiomatizable by
is axiomatizable by ![]() -formulas.
-formulas.
b) If ![]() , then
, then ![]() is axiomatizable by disjunctions of
is axiomatizable by disjunctions of ![]() -formulas.
-formulas.
Proof.
a) Let ![]() and
and ![]() . As
. As ![]() , we have
, we have ![]() yielding a
yielding a ![]() with
with ![]() which shows by hypothesis that
which shows by hypothesis that ![]() .
.
b) Let ![]() and
and ![]() . We want to show
. We want to show ![]() .
.
Define ![]() and
and ![]() . Then
. Then ![]() , so
, so ![]() , meaning that there is an
, meaning that there is an ![]() for which
for which ![]() .
.
Now use the hypothesis for model ![]() : there is a
: there is a ![]() , so that
, so that ![]() . But it can’t be in
. But it can’t be in ![]() because
because ![]() , so
, so ![]() , yielding
, yielding ![]() thus
thus ![]() .
.
This theorem proves one direction in all of the above mentioned preservation theorems.
The converse direction, that the specific types of formulas are preserved under the specific operator on the class of models is a straightforward verification in each case.
However, we can prove a common generalization for them, using the more specific logic described in this post.
Let ![]() be an arbitrary profunctor with an initial object
be an arbitrary profunctor with an initial object ![]() , objects of
, objects of ![]() regarded as ‘situations’ and objects of
regarded as ‘situations’ and objects of ![]() as ‘models’, and introduce the relation ‘diagonal fill-in‘ (or ‘left lifting property‘) between arrows of
as ‘models’, and introduce the relation ‘diagonal fill-in‘ (or ‘left lifting property‘) between arrows of ![]() and arrows of
and arrows of ![]() as follows:
as follows:
![]()
that is, iff every commutative square with ![]() on the top and
on the top and ![]() on the bottom has a diagonal fill-in
on the bottom has a diagonal fill-in ![]() making the whole diagram commutative:
making the whole diagram commutative:
![Rendered by QuickLaTeX.com \[\dia{\ar[r]^\alpha \ar[d]_u & \ar[d]^v \ar@{-->}[ld]|d \\\ar[r]_f &}\]](https://profunctors.zellerede.tk/wp-content/ql-cache/quicklatex.com-d2cccd2d437090d4692ca6e4966483b0_l3.png)
For a subclass of morphisms
For example, in the first order case, we have![]() surjective morphisms of
surjective morphisms of ![]() , and
, and![]() injective morphisms of
injective morphisms of ![]() .
.
Moreover,![]() whenever
whenever ![]() , and
, and![]() whenever
whenever ![]() and
and ![]() consists only of equations.
consists only of equations.
Universal formulas correspond to those trees in which Eve doesn’t select new variables (so that the ![]() part doesn’t change in arrows on odd levels), and positive formulas correspond to trees in which
part doesn’t change in arrows on odd levels), and positive formulas correspond to trees in which Adam doesn’t select new relations or equations to hold (so that the ![]() part is empty in the root situation and doesn’t change in arrows on even levels).
part is empty in the root situation and doesn’t change in arrows on even levels).
Theorem. Let ![]() be an arbitrary class of morphisms in
be an arbitrary class of morphisms in ![]() , and let
, and let ![]() be a tree in which every arrow
be a tree in which every arrow Eve can possibly choose is in ![]() . Then
. Then ![]() implies
implies ![]() .
.
Dually, if ![]() is of the above form, then
is of the above form, then ![]() implies
implies ![]() .
.
It turns out that examples 1. and 2. above have a common generalization in this setting.
Theorem. Let ![]() be a functor, surjective on hom-sets, suppose
be a functor, surjective on hom-sets, suppose ![]() has pushouts and assume that a class
has pushouts and assume that a class ![]() of morphisms is defined by a set
of morphisms is defined by a set ![]() of arrows by the diagonal-fill-in relation:
of arrows by the diagonal-fill-in relation: ![]() .
.
Then the relation between objects ![]() stating
stating ![]() is modelwise expressible by trees in which the arrows that
is modelwise expressible by trees in which the arrows that Adam might choose are all ![]() in the profunctor
in the profunctor ![]() .
.
Proof. Since ![]() is opfunctorial, every
is opfunctorial, every ![]() has a coreflection arrow
has a coreflection arrow ![]() , which is now also a pre-reflection: each heteromorphism
, which is now also a pre-reflection: each heteromorphism ![]() factors through (not necessarily uniquely)
factors through (not necessarily uniquely) ![]() , because of the surjectivity condition.
, because of the surjectivity condition.
For all ![]() and arrow
and arrow ![]() , fix a pushout square
, fix a pushout square ![]() and collect all such
and collect all such ![]() ‘s in a class
‘s in a class ![]() . Note that from each
. Note that from each ![]() there starts out only set-many arrows of
there starts out only set-many arrows of ![]() , and also note that
, and also note that ![]() holds because
holds because ![]() is a pushout of
is a pushout of ![]() .
.
For a given ![]() , consider the following tree:
, consider the following tree:
![Rendered by QuickLaTeX.com \[\dia{&&&& \ar[r]^r_{}="U" & m^\Delta \ar@{}[d]|{\displaystyle{m^\Delta}}="R" \ar[l];"R"^{}="V" \ar@{}"U";"V"|: & : cr=1_{m^\Delta}\\\delta_m & := & 0\ar[r]& m^\Delta \ar[ur]^c_{}="A" \ar[r]|{}="B" \ar[dr]^{}="C" \ar@{}"A";"B"|\vdots \ar@{}"B";"C"|\vdots^{\in C} &&\\&&&&&}\]](https://profunctors.zellerede.tk/wp-content/ql-cache/quicklatex.com-2b7b174bd9965bab6f8943601478465f_l3.png)
where every arrow
Adam) and the next layer of the tree consists of all right inverses Proving ![]() is straightforward after letting
is straightforward after letting Eve choose the coreflection arrow ![]() .
.
Now, assume ![]() for an arbitrary object
for an arbitrary object ![]() . We want to show the existence of an arrow
. We want to show the existence of an arrow ![]() .
.
Let’s call ![]() the interpretation
the interpretation Eve chooses on ![]() . By hypothesis,
. By hypothesis, ![]() is also a pre-reflection arrow, yielding an arrow
is also a pre-reflection arrow, yielding an arrow ![]() such that
such that ![]() . We show
. We show ![]() .
.
Let ![]() and assume a commutative square
and assume a commutative square 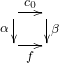 is given. Since
is given. Since ![]() is a coreflection arrow, there is a (unique)
is a coreflection arrow, there is a (unique) ![]() such that
such that ![]() . Then use the chosen pushout of
. Then use the chosen pushout of ![]() and
and ![]() to form
to form
![Rendered by QuickLaTeX.com \[\dia{x \ar@/_1pc/[dd]_\alpha \ar[r]^{c_0} \ar[d]^{\alpha_1} & y \ar@/^1pc/[dd]^\beta \ar[d]_t \\ m^\Delta \ar[r]^c \ar[d]|j \ar[rd]_u & \ar@{}[lu]|(.14){\displaystyle{\ulcorner}} \ar[d]|(.4){\beta_1} \\m \ar[r]_f & a }\]](https://profunctors.zellerede.tk/wp-content/ql-cache/quicklatex.com-fc3959ccb8667ba18959cd7df57cd17c_l3.png)
and let
Adam choose branch Eve‘s answer branch with interpretation forced to be This is going to work as a diagonal-fill-in in the originally given square
 .
.
