A Bridge Construction – Profunctors

A category $\ct H$ is a bridge between categories $\ct A$ and $\ct B$ if these are disjoint full subcategories of $\ct H$ and $\ct H$ has no more objects. In notation: $\ct H:\ct A \rightleftharpoons \ct B$ .

In other words, if $\ct Iso$ denotes the category of 2 objects (name them $0,1$ ) and 2 nonidentity arrows, ${\bf i}:0\to 1,\ {\bf j}:1\to 0$ which are inverses of each other, then a bridge is a category over $\ct Iso$ , i.e. a category $\ct H$ equipped with a functor $H:\ct H\to\ct Iso$ . The full subcategories $\ct A:=H^{-1}(0)$ and $\ct B:=H^{-1}(1)$ are called banks of the bridge.
The arrows in the $H$ -preimage of the two arrows ${\bf i}$ and ${\bf j}$ in $\ct Iso$ are referred to as through arrows or heteromorphisms in the bridge.

Throughout the note, letters $a,\,a',\,a_0,\dots$ denote objects of $\ct A$ and letters $b,\,b',\,b_0,\dots$ denote objects of $\ct B$ .

Note that if there are no heteromorphisms of the form $b\to a$ , or if we delete them, then we receive a profunctor $\ct A\ag\ct B$ that we denote by $\ct H^>$ . We define $\ct H^<:\ct B\ag\ct A$ similarly.
Also note that a bridge is thus built up by these two profunctors $\ct H^>$ and $\ct H^<$ , connected by a so called Morita context which is exactly the structure that is needed to provide composition of consecutive zigzag heteromorphisms, i.e. those of the form $a\to b\to a'$ or $b\to a\to b'$ .
Since both banks are assumed to be full subcategories, these zigzag compositions must exist purely within the bank $\ct A$ or $\ct B$ .

Examples

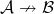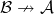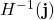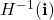As mentioned, any profunctor $\ct A\ag\ct B$ or $\ct B\ag\ct A$ is in particular, a bridge, where either $H^{-1}({\bf j})$ or $H^{-1}({\bf i})$ empty.
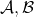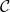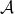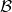Any two full subcategories $\ct A,\ct B$ of a category $\ct C$ determines a bridge by taking disjoint copies of $\ct A$ and $\ct B$ and adding heteromorphisms from $\ct C$ .
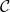To give a specific example, we obtain a bridge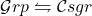 $\ct Grp\leftrightharpoons\ct Csgr$ between groups and commutative semigroups with semigroup homomorphisms as heteromorphisms.
In particular, every category 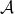$\ct A$ has an identity bridge 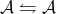$\ct A\leftrightharpoons\ct A$ where every object is duplicated and every morphism is present in 4 instances. Note that this, as a category, is equivalent to $\ct A$ itself.

The construction

Given an arbitrary profunctor $\ct F:\ct A\ag\ct B$ , we can formally invert those heteromorphisms which are both reflection and coreflection arrows at once.

So, we can define a bridge $\ct F[\Theta^{-1}]$ for any
$\Theta\subseteq\{\vartheta:a\to b \mid \vartheta\,\text{ is both reflection and coreflection arrow}\}$
by adding heteromorphisms $b\to a$ of the form $(\underset{b\to b'}\beta,\underset{a'\to b'}\vartheta,\underset{a'\to a}\alpha)$ , which would represent the formal composition $\beta\vartheta^{-1}\alpha$ , where we need to regard the formal compositions $\vartheta^{-1}\alpha$ and $\beta\theta^{-1}$ equal whenever $\alpha\theta=\vartheta\beta$ and $\theta,\vartheta\in\Theta$ . and we need to consider every consequences of these equations.
In other words, we quotient out by the smallest equivalence relation that is closed under compositions and generated by all pairs $\left(\,(1_b,\vartheta,\alpha),\ (\beta,\theta,1_a)\,\right)$ that satisfy $\alpha\theta=\vartheta\beta$ .

$\NZT{}\vartheta b\alpha{}\beta a\theta{}$

Assume $\upsilon:a_0\to b'$ and $\tau:a'\to b_1$ are heteromorphisms, then the following compositions are defined by means of the unique arrow in $\ct A$ [resp. in $\ct B$ ] that exists by the coreflection [resp. reflection] property of $\vartheta$ to make the diagrams commutative:

$\dia@=1.2pc{&& a_0\ar[rd]^{\upsilon} \ar@{.>}[dd]_{\exists!\, \xi} &\\\upsilon\cdot(\beta,\vartheta,\alpha):=\xi\alpha && &b' \ar[d]^{\beta} &&(\beta,\vartheta,\alpha)\cdot\tau:=\beta\eta\\ && a\ar[r] \ar[r]^{\vartheta} \ar[d]_{\alpha}& b \ar@{.>}[dd]^{\exists!\, \eta} \\&& a' \ar[rd]_{\tau} \\ && & b_1}$

Examples

4. Consider the category $\ct Mat$ whose objects are natural numbers and arrows $n\to m$ are $n\times m$ matrices over a given field $k$ , composition is matrix multiplication. We can define a natural profunctor $\ct E:\ct Mat\ag\ct Vect$ to the category of vector spaces over $k$ , by setting a through arrow $n\to V$ to be an $n$ -tuple of elements of $V$ , i.e. $\ct E(n,V)=V^n$ .
Compositions are defined straightforwardly. A through arrow $(v_1,\dots,v_n):n\to V$ will be a reflection and coreflection arrow at once iff it is a basis of $V$ .
Applying the bridge construction, we receive a category where the object $n$ is effectively isomorphic to every $n$ dimensional vector space.

5. Let $\ct P:\ct Set\ag\ct Bool^{op}$ be the profunctor with heteromorphisms $S\to B$ the element-like relations $\eps\subseteq S\times B$ , i.e. those that satisfy
$\bullet\quad$ $s\,\eps\, 1_B$ for the maximal element $1_B$ of the Boolean algebra $B$
$\bullet\quad$ if not $s\,\eps\, a$ then $s\,\eps\, \lnot a$
$\bullet\quad$ if $s\,\eps\, a$ and $s\,\eps\, b$ then $s\,\eps\,(a\land b)$
for all elements $s\in S$ and $a,b\in B$ .
We compose $\underset{S\to S'-B'\leftarrow B}{f\ \ \eps\ \ h}$ by defining

$s\,(f\eps h)\, b\ \iff\ s^f\,\eps\, b^h \,.$

If $S$ is a finite set, $P(S)$ is its power set, then the element relation $\in$ is a reflection-coreflection arrow.