A profunctor ![]() is functorial iff every object of
is functorial iff every object of ![]() has a reflection in
has a reflection in ![]() within
within ![]() . Fixing (arbitrarily) one reflection arrow for each object
. Fixing (arbitrarily) one reflection arrow for each object ![]() yields a functor
yields a functor ![]() such that
such that ![]() .
.
Dually, ![]() is co-functorial iff every object of
is co-functorial iff every object of ![]() has a coreflection in
has a coreflection in ![]() , yielding a functor
, yielding a functor ![]() such that
such that ![]() .
.
If both are satisfied, then ![]() above is left adjoint to
above is left adjoint to ![]() .
.
This analogy continues in dimension 2 (for bicategories or double categories), yielding the colax functors as double profunctors with the reflection property and the lax functors as double profunctors with the coreflection property. If a double profunctor has both property, it determines a colax/lax adjunction.
Double categories
A double category consists of objects (![]() ), vertical arrows (
), vertical arrows (![]() ), horizontal arrows (
), horizontal arrows (![]() ), and cells (
), and cells (![]() ). Each arrow is assigned its start and end point, as two (not necessarily distinct) objects, called the ‘domain’ and ‘codomain’. Each cell is assigned its boundary
). Each arrow is assigned its start and end point, as two (not necessarily distinct) objects, called the ‘domain’ and ‘codomain’. Each cell is assigned its boundary ![]() , depicted as
, depicted as
![Rendered by QuickLaTeX.com \[\nzt fu\alpha vg\]](https://profunctors.zellerede.tk/wp-content/ql-cache/quicklatex.com-c475940ed59ee31e3cc940c07f53f0c2_l3.png)
There is a horizontal composition on the horizontal arrows
The compositions has identity elements: each object determines a horizontal and a vertical identity [denoted by
And finally, the compositions are associatve: the vertical compositions are assumed to be strictly associative:
Examples:
- Any category can be seen as a double category, with the arrows playing the role of both vertical and horizontal arrows, and the cells being the commutative squares.
- Any bicategory naturally determines a double category, in which the only vertical arrows are the identities. Thus all things written below are valid as well for (co)lax functors between bicategories.
- We can consider the double category
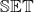 of sets, with vertical arrows the functions
of sets, with vertical arrows the functions 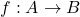 and with horizontal arrows the binary relations
and with horizontal arrows the binary relations 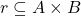 , having a unique cell with border
, having a unique cell with border 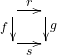 iff
iff 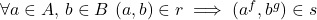 .
. - In the double category of rings, the objects are the rings, the vertical arrows are ring homomorphisms, the horizontal arrows are the bimodules with composition the tensor product, and a cell
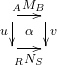 is a map
is a map 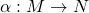 which preserves addition and satisfies
which preserves addition and satisfies 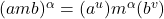 for all
for all 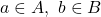 .
. - In the double category of categories the objects are the categories, the vertical arrows are functors, the horizontal arrows are the profunctors, and a cell
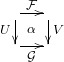 is simply a functor
is simply a functor 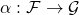 such that
such that 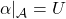 and
and 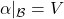 , where profunctors are regarded as categories (over the arrow), as in our profunctor post.
, where profunctors are regarded as categories (over the arrow), as in our profunctor post.
Let ![]() be a double category. Then, as vertical composition (either of vertical morphisms or of cells) is strictly associative, we obtain
be a double category. Then, as vertical composition (either of vertical morphisms or of cells) is strictly associative, we obtain
- a category
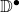 with the same objects as
with the same objects as 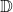 and the vertical arrows as arrows (hence forgetting horizontal arrows and cells)
and the vertical arrows as arrows (hence forgetting horizontal arrows and cells) - a category
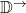 with horizontal arrows as objects and cells with vertical composition as arrows (forgetting only the horizontal compositions)
with horizontal arrows as objects and cells with vertical composition as arrows (forgetting only the horizontal compositions)
Accordingly, the notation ![]() means that
means that ![]() is a horizontal arrow of
is a horizontal arrow of ![]() .
.
Double profunctors
Let ![]() and
and ![]() be double categories. Then a double profunctor from
be double categories. Then a double profunctor from ![]() to
to ![]() can be defined as a double category
can be defined as a double category ![]() , disjointly containing (isomorphic copies of)
, disjointly containing (isomorphic copies of) ![]() and
and ![]() , such that any further cell has a boundary
, such that any further cell has a boundary ![]() with
with ![]() and
and ![]() . These additional cells are called ‘heterocells‘ or ‘through cells‘, and
. These additional cells are called ‘heterocells‘ or ‘through cells‘, and ![]() are the (necessarily vertical) ‘heteromorphisms‘ or ‘through arrows‘.
are the (necessarily vertical) ‘heteromorphisms‘ or ‘through arrows‘.
(Alternatively, a double profunctor can be viewed as a strict functor ![]() where
where ![]() is the ‘vertical arrow’ double category, containing 2 objects,
is the ‘vertical arrow’ double category, containing 2 objects, ![]() and a single nonidentity vertical arrow
and a single nonidentity vertical arrow ![]() .)
.)
Recall that an arrow ![]() in a category is a reflection arrow to a subcategory
in a category is a reflection arrow to a subcategory ![]() if
if ![]() and for every
and for every ![]() , there is a unique
, there is a unique ![]() such that
such that ![]() .
.
Definition. A double profunctor ![]() has the reflection property, if there are a collection
has the reflection property, if there are a collection ![]() of heteromorphisms and a collection
of heteromorphisms and a collection ![]() of heterocells, such that
of heterocells, such that
a) each ![]() is a reflection arrow from
is a reflection arrow from ![]() to
to ![]() within
within ![]() ,
,
b) for every horizontal ![]() , the boundary of
, the boundary of ![]() is of the form
is of the form ![]() for some
for some ![]() ,
,
c) and each ![]() is a reflection arrow from
is a reflection arrow from ![]() to
to ![]() within
within ![]() .
.
The main observation is that these already induce the following comparison cells:
- For any
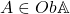 , the horizontal identity cell
, the horizontal identity cell 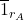 of
of 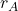 uniquely factors through
uniquely factors through 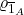 , i.e. there is a cell
, i.e. there is a cell 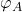 such that
such that 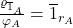 .
.
By b) it follows that the left and right side of the boundary of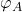 must be vertical identities, also its bottom is a horizontal identity.
must be vertical identities, also its bottom is a horizontal identity. - For any consecutive horizontal arrows
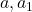 in
in 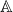 , the horizontal composition
, the horizontal composition 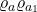 uniquely factors through
uniquely factors through 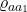 , yielding a cell
, yielding a cell 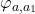 such that
such that 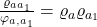 .
.
Based on similar considerations as above, if we write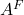 for the codomain of
for the codomain of 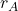 and
and 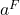 for the bottom of
for the bottom of 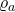 , then the boundary of
, then the boundary of 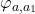 is
is 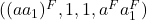 .
.
That is, what this data describes is nothing else but a colax functor.
We can also convert this (assuming choice, of course): it is not hard to construct a double profunctor for any colax functor by adding formal heteroarrows and heterocells and defining their horizontal composition using the comparison cells.
Dually, a double profunctor with the coreflection property is basically a lax functor.
And, if a double profunctor has both the reflection and the coreflection property, then the corresponding colax and lax functors determine a so called colax/lax adjunction.
Examples:
- Consider the forgetful functor from unital rings to monoids (which forgets addition), and extend it to their bimodules and biacts. This way we obtain a lax functor
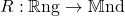 . The vertical heteromorphisms in the corresponding double profunctor
. The vertical heteromorphisms in the corresponding double profunctor 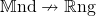 are the monoid morphisms from a monoid to (the underlying multiplicative monoid of) a ring, and the heterocells are the biact morphisms from a biact to a bimodule. More explicitly, each heterocell
are the monoid morphisms from a monoid to (the underlying multiplicative monoid of) a ring, and the heterocells are the biact morphisms from a biact to a bimodule. More explicitly, each heterocell 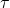 has a boundary
has a boundary
where![Rendered by QuickLaTeX.com \[\NZT AUBf{}gRMS\]](https://profunctors.zellerede.tk/wp-content/ql-cache/quicklatex.com-f2e602d4b631b6725e4f5886f95d14e5_l3.png)
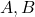 are monoids,
are monoids, 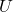 is an
is an 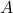 –
–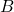 -biact,
-biact, 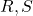 are unital rings,
are unital rings, 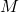 is an
is an 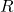 –
–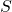 -bimodule,
-bimodule, 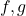 are vertical heteromorphisms. Then
are vertical heteromorphisms. Then 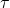 is simply a function
is simply a function 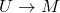 that satisfies
that satisfies 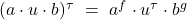 for all
for all 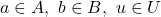 .
. - We obtain a double profunctor
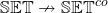 by binary relations as vertical heteromorphisms. Here a heterocell
by binary relations as vertical heteromorphisms. Here a heterocell 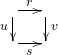 has each side as a binary relation, and a single heterocell exists with such boundary iff we get both containment of (left-to-right) compositions
has each side as a binary relation, and a single heterocell exists with such boundary iff we get both containment of (left-to-right) compositions 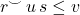 and
and 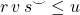 where superscript
where superscript  means to reverse the relation.
means to reverse the relation.
The reflection of an object, i.e. a set , is its power set
, is its power set 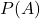 with the
with the  relation as the reflection arrow, and the reflection of a horizontal arrow, i.e. a relation
relation as the reflection arrow, and the reflection of a horizontal arrow, i.e. a relation 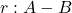 is the relation
is the relation 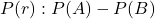 between the power sets that holds for a pair
between the power sets that holds for a pair 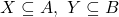 iff
iff 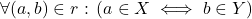 .
.
[1] “Bridges and Profunctors”, PhD dissertation, Bertalan Pécsi
