Plenty faces of a profunctor

What is a profunctor?

Recall that a category is a directed graph equipped with an associative and unital composition of its edges. In the categorical context, the nodes of the graph are also called objects and edges are called arrows or morphisms. The unitality requirement says that each object $a$ has a unit arrow $a\to a$ , called identity, which doesn’t affect the result of the compositions.

A functor is a composition and identity preserving graph morphism from a category to a category.

A profunctor, on the other hand, connects up two categories by (potentially) adding more morphisms in between them ‘from the outer world’. In other perspective, we can describe this setting as one of the two categories acting from the left and the other one acting from the right on the newly added morphisms. This can also be grasped as simply being a two variable functor to the category of sets, contravariant in the first argument.

Here we collected some definitions, each being equivalent to each other, in the sense that the given ‘structures’ can be uniquely transformed into each other.

In what follows, let $\ct A$ and $\ct B$ be two categories.

Def.1. A category $\ct F$ is called a profunctor between $\ct A$ and $\ct B$ , if it disjointly and fully contains (isomorphic copies of) $\ct A$ and $\ct B$ and any other arrow of $\ct F$ goes from an object of $\ct A$ to an object of $\ct B$ .
Such arrows of $\ct F$ are called heteromorphisms or through arrows.

So, a profunctor connects up $\ct A$ and $\ct B$ by adding heteromorphisms of the form $a\to b$ which can be (interchangeably) composed by morphisms of $\ct A$ from the left and by morphisms of $\ct B$ from the right, in order to make $\ct F$ itself a category.

Let’s see some examples. Naturally, all these can be interpreted as examples for any definition in this post.
Example 1. Let $\ct A$ be the category of sets and $\ct B$ the category of groups, and let the heteromorphisms $S\to G$ from a set $S$ to a group $G$ be the functions from $S$ to (the underlying set of) $G$ . Composition is function composition.

Example 2. Let $k$ be a field and $V$ be a fixed vector space over $k$ , and let $\ct A$ and $\ct B$ be both the category of $k$ -vector spaces. Let the heteromorphisms $U\to W$ be the bilinear maps $U\times V\to W$ . Compositions can be straightforwardly defined.

Example 3. Let $\ct A$ be the category of sets, and let $\ct B$ be its opposite category, and let the heteromorphisms $A\to B$ be the relations $\subseteq A\times B$ , with composition for functions $f:A'\to A,\ g:B'\to B$ and relation $u\subseteq A\times B$ :

$a'\,\overset{fug}{-}\,b'\ \iff\ (a')^f\,\overset{u}{-}\,(b')^g\,.$

The above examples are all adjoint profunctors, presenting an adjoint situation of two functors by reflections and coreflections in themselves. We present a general construction of examples towards the end of this post.

Let $\bf 2$ denote the arrow category which has two objects, call them $0$ and $1$ , and a single nonidentity arrow $0\to 1$ .
Def.2. A profunctor from $\ct A$ to $\ct B$ is a category over the arrow, i.e. it is a functor $p:\ct F\to{\bf 2}$ for some category $\ct F$ , equipped with pullback diagrams

$\PUB{\ct A}{}{\ct F}{}{}p{\bf 1}0{\bf 2}\ \Quad \ \Quad\ \PUB{\ct B}{}{\ct F}{}{}p{\bf 1}1{\bf 2}\ .$

So that, the left and right base categories $\ct A$ and $\ct B$ are basically just the inverse images $\ct A\cong p^{-1}(0),\ \ \ct B\cong p^{-1}(1)$ of objects $0$ and $1$ of $\bf 2$ along $p$ , respectively (and of their identities), up to isomorphism of categories.

Importantly, the $p$ -preimage of the arrow $0\to 1$ consists exactly of the heteromorphisms of $\ct F$ .

Def.3. A profunctor is a functor $\ct A^{op}\times\ct B\to\ct Set$ .
It simply assigns the set of heteromorphisms $a\to b$ to the object pair $(a,b)\in Ob\ct A^{op}\times\ct B$ , and assigns the function $f\mapsto \alpha f\beta$ to the morphism pair $(\alpha,\beta)\in \ct A^{op}\times\ct B$ .
In other words, given the category $\ct F$ as above, take its hom functor $\ct F^{op}\times\ct F\to\ct Set$ and restrict it to $\ct A^{op}\times\ct B$ .
Conversely, a given functor $F:\ct A^{op}\times\ct B\to\ct Set$ determines a category $\ct F$ by adding the elements of $F(a,b)$ regarding them as heteromorphisms $a\to b$ , and by defining the compositions $\alpha\cdot f\cdot\beta$ as the image of $f$ under the function $F(\alpha,\beta)$ .

A span between sets $A$ and $B$ is a pair of functions $s:E\to A$ , $t:E\to B$ for some set $E$ .
This can be visualized as a kind of bipartite graph between $A$ and $B$ , the elements of $E$ being the edges, and $s$ assigns their sources from $A$ while $t$ assigns their targets from $B$ .
Note, however that $A$ and $B$ as sets may overlap, in particular, we allow $A=B$ , when a span becomes exactly a directed graph (or quiver), having the starting and end points of the edges in the same set.
In other perspective, a span associates the set of edges from $a$ to $b$ for a given pair $a\in A,\ b\in B$ . Said that, a span is none other than a ‘function’ $A\times B\to Set$ : a profunctor at the level of sets.

Spans can be ‘composed‘ as follows:
Let $\ct E:A\ot E\to B$ and $\ct F:B\ot F\to C$ be two spans. Their composite span $\ct E\ct F$ between $A$ and $C$ consists of all $2$ length paths of the form $\z e,f\x$ with $e\in E,\ f\in F$ .

This way, spans are organized in a bicategory structure as arrows between sets. Bicategories provide a level of abstraction where general left and right actions can be nicely defined and studied, by means of their ‘internal monoids‘ (also called monads in this context).
An internal monoid in a bicategory is, roughly, an arrow $M:a\to a$ equipped with an ‘associative, unital operation’ $\mu:MM\to M$ .

The internal monoids in the bicategory of spans turn out to be just the categories.

A left action of an internal monoid $M:a\to a$ on an arrow $U:a\to b$ is a $MU\to U$ which is compatible with $\mu$ . A right action can be dually defined.
If $M:a\to a$ and $N:b\to b$ are monoids, a bimodule between them is an arrow $U:a\to b$ equipped with a left and a right action at once, compatible with each other, in the sense that they provide a unique two sided action $MUN\to U$ .

Def.4. A profunctor is a bimodule in the bicategory of spans.

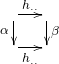Construction. Any subcategory $\ct D$ of $\ct A\times\ct B$ can be seen as a categorical relation between $\ct A$ and $\ct B$ , and any such induces a profunctor from $\ct A$ to $\ct B$ by freely adjoining a new heteromorphism $h_{a,b}:a\to b$ whenever $(a,b)\in Ob\ct D$ and forcing all squares $\nzt{h_{..}}\alpha{}\beta{h_{..}}$ to commute whenever $(\alpha,\beta)\in\ct D$ .
Any functor is a categorical relation, and so is the opposite relation of any categorical relation, i.e. when $\ct A$ and $\ct B$ and the freely added arrows are swapped.

Example 4. Apply the above construction for the singleton subcategory containing only $(a,b)$ (and its identity) for any fixed pair of objects $a\in Ob\ct A,\ b\in Ob\ct B$ .
Then we receive a profunctor $\ct H_{a,b}$ which satisfies

$\ct H_{a,b}(a',\,b')\,\cong\,\ct A(a',a)\times \ct B(b,b')$

as each heteromorphism $a'\to b'$ can uniquely be written as $\alpha\cdot h_{a,b}\cdot\beta$ with $\alpha:a'\to a,\ \beta:b\to b'$ , by construction.

(to be continued with…)
Let $\hat{\ct\ct A}$ denote the category of right modules over a category $\ct A$ , i.e. the category of profunctors ${\bf 1}\ag\ct A$ . These are also known as the presheaves over $\ct A\op$ .
A functor is said to be cocontinuous if it preserves arbitrary colimits.

Def.5. A profunctor $\ct A\ag\ct B$ is a cocontinuous functor $\hat{\ct A}\to\hat{\ct B}$ .