In topology, any continuous function ![]() can be considered as a fibration over space
can be considered as a fibration over space ![]() , with total space
, with total space ![]() , where the fibres
, where the fibres ![]() are glued together according to the topology of
are glued together according to the topology of ![]() .
.
Likewise, any functor ![]() can be regarded as a kind of fibration over
can be regarded as a kind of fibration over ![]() . Each object
. Each object ![]() determines a fibre category
determines a fibre category ![]() with arrows which are mapped to
with arrows which are mapped to ![]() .
.
In this generality, the fibres connect up by means of profunctors between them and then ![]() and the original composition of
and the original composition of ![]() are encapsulated in the arising mapping
are encapsulated in the arising mapping ![]() .
.
More specifically, given any arrow ![]() , its preimage
, its preimage ![]() determines [is] a profunctor between categories
determines [is] a profunctor between categories ![]() and
and ![]() , all within
, all within ![]() .
.
For a composable pair of arrows ![]() , we obtain a comparison map
, we obtain a comparison map ![]() , which is just the composition defined in
, which is just the composition defined in ![]() of the occuring pairs of arrows.
of the occuring pairs of arrows.
The comparison maps make this mapping ![]() a ‘normal lax functor’.
a ‘normal lax functor’.
Under certain hypothesis on ![]() , all the arising profunctors become functorial (when each object from the source category has a reflection on the target category), yielding a normal lax functor
, all the arising profunctors become functorial (when each object from the source category has a reflection on the target category), yielding a normal lax functor ![]() . Such an
. Such an ![]() is called an opposite Grothendieck prefibration. The reflection arrows are also called (weak) cartesian morphisms of
is called an opposite Grothendieck prefibration. The reflection arrows are also called (weak) cartesian morphisms of ![]() .
.
If they are closed under composition in ![]() , the comparison maps become invertible, so that composition of the profunctors is preserved (up to isomorphism), then we talk about Grothendieck opfibration.
, the comparison maps become invertible, so that composition of the profunctors is preserved (up to isomorphism), then we talk about Grothendieck opfibration.
Its dual notion, when all profunctors are opfunctorial, is the Grothendieck (pre-)fibration.
Finally, as a bonus, we illustrate here the post Co/lax functors without apriori comparison cells for the general case of an arbitrary functor ![]() , by constructing a double profunctor
, by constructing a double profunctor ![]() that corresponds to the arising lax functor
that corresponds to the arising lax functor ![]() .
.
Consider the full sub-bicategory of ![]() on certain particular subcategories of
on certain particular subcategories of ![]() as objects, namely, the fibres
as objects, namely, the fibres ![]() for each object
for each object ![]() . Fix a unique vertical heteromorphism
. Fix a unique vertical heteromorphism ![]() for each
for each ![]() . All these are only required to support the heterocells
. All these are only required to support the heterocells 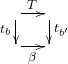 which are defined to be the profunctor morphisms
which are defined to be the profunctor morphisms ![]() , where
, where ![]() is an arbitrary profunctor.
is an arbitrary profunctor.
The horizontal composition of given heterocells ![]() and
and ![]() with arrows
with arrows ![]() of
of ![]() is given by
is given by
![]()
where
