Given categories 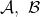 and objects
and objects 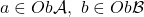 , we let
, we let 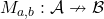 denote the category where we freely add an arrow
denote the category where we freely add an arrow 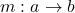 to the disjoint union of
to the disjoint union of 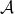 and
and 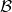 .
.
This can be achieved e.g. by taking the colimit of the following 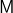 -shaped diagram:
-shaped diagram:
![Rendered by QuickLaTeX.com \[\dia@R=1pc{{\bf 1}\ar[rd]^0 \ar[dd]_a && {\bf 1} \ar[ld]_1 \ar[dd]^b \\ & {\bf 2} & \\ \ct A && \ct B}\]](https://profunctors.zellerede.tk/wp-content/ql-cache/quicklatex.com-09a37fbaad357fb503211e122fd31be8_l3.png)
where
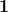
is the terminal category and
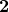
contains two objects, denoted by
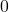
and
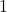
, and a single nonidentity arrow
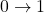
, whose image in the colimit will be the freely adjoined arrow
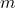
.
Alternatively, we can consider the profunctor induced by the span
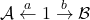
(which is just the profunctor composition
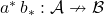
).
It’s straightforward to check that 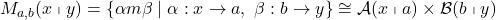 .
.
Based on the construction, for any profunctor 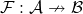 , the profunctor morphisms
, the profunctor morphisms 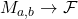 (functors that are identical on both
(functors that are identical on both  and
and  ) are uniquely determined by where they take the freely added arrow
) are uniquely determined by where they take the freely added arrow 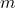 , and that can be any heteromorphism
, and that can be any heteromorphism 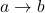 in
in 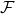 .
.
Theorem. (Yoneda lemma for profunctors.) For any profunctor 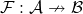 and objects
and objects 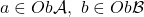 we have a bijection
we have a bijection
![Rendered by QuickLaTeX.com \[\ct Prof(M_{a,b}\ig \ct F)\,\cong\,\ct F(a\ig b)\]](https://profunctors.zellerede.tk/wp-content/ql-cache/quicklatex.com-acd9f8b0b7304b5d932819ae3be0861a_l3.png)
natural in both

and
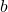
.
It’s also straightforward to verify that, for profunctors 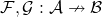 , a functor
, a functor 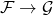 that acts as the identity on both
that acts as the identity on both 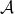 and
and 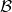 , naturally corresponds to a natural transformation
, naturally corresponds to a natural transformation  where
where 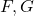 are the hom functors of
are the hom functors of 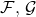 restricted to heteromorphisms (i.e.
restricted to heteromorphisms (i.e. 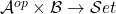 ), and vice-versa.
), and vice-versa.
This way, involving our previous observation about 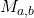 , we can reformulate the above theorem as, for any functor
, we can reformulate the above theorem as, for any functor 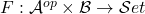 we have
we have
![Rendered by QuickLaTeX.com \[Nat(\ct A(-,a)\times\ct B(b,-)\ig F)\,\cong\, F(a,b)\]](https://profunctors.zellerede.tk/wp-content/ql-cache/quicklatex.com-17006ea7aa43d968937b9a2e24be700f_l3.png)
naturally in
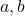
.
That clearly implies both the covariant and the contravariant versions of the original Yoneda lemma when applying it either with 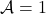 or with
or with 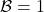 .
.
Presheaves as simple extensions
A presheaf on a category 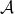 is a functor
is a functor 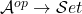 , so using
, so using 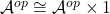 we can even consider it as a profunctor
we can even consider it as a profunctor 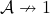 , which can be viewed as a left
, which can be viewed as a left 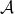 -module, or… as a simple right extension of
-module, or… as a simple right extension of 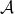 by a single object (the object of
by a single object (the object of 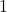 ).
).
Similarly, a presheaf on the opposite category 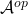 can be though of as a right
can be though of as a right 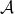 -module, or as a simple left extension.
-module, or as a simple left extension.
Definition. A category 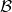 with object
with object 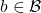 is a simple right extension of category
is a simple right extension of category 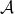 by a new object
by a new object 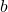 , if
, if 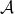 is a full(y embedded) subcategory of
is a full(y embedded) subcategory of 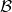 ,
, 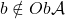 ,
, 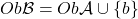 and
and 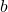 is not the domain of any morphism besides its identity
is not the domain of any morphism besides its identity 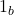 .
.
Examples. For any object  we obtain a simple right extension by joining a new object
we obtain a simple right extension by joining a new object 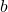 and copying all the arrows
and copying all the arrows 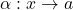 as
as 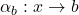 where
where  . This extension category will be denoted by
. This extension category will be denoted by 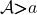 .
.
Observe that by construction, 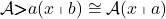 , so it’s just the hom functor
, so it’s just the hom functor 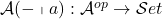 seen as a profunctor
seen as a profunctor 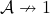 where
where 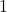 is embedded into
is embedded into 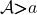 as the new object
as the new object 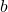 .
.
We can also define the empty and the unique simple right extensions by prescribing that each 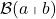 contains exactly 0 or 1 elements, respectively.
contains exactly 0 or 1 elements, respectively.
If 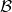 and
and 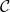 are simple right extensions of
are simple right extensions of 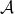 , with new objects
, with new objects 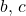 , respectively, then a functor
, respectively, then a functor 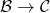 is said to be a morphism of extensions whenever it takes
is said to be a morphism of extensions whenever it takes 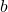 to
to  and fixes all objects and arrows in
and fixes all objects and arrows in 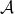 .
.
Theorem. (Yoneda lemma for simple right extensions.)
For every simple right extension 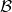 of
of 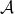 , the morphisms of extensions
, the morphisms of extensions 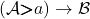 correspond to the new arrows
correspond to the new arrows 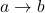 in
in 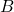 , naturally in
, naturally in 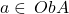 .
.
Proof. Such a morphism is uniquely determined by where it takes the copy of 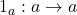 in
in 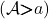 and that can be any new arrow
and that can be any new arrow 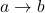 .
.
Theorem. (co-Yoneda lemma for simple right extensions.)
Every simple right extension 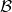 of
of 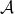 is a colimit of simple extensions
is a colimit of simple extensions 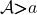 .
.
Proof. Let a simple right extension 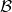 of
of 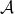 with new object
with new object 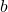 be fixed, and consider the following diagram
be fixed, and consider the following diagram 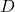 on the slice category
on the slice category 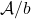 : an object of that is a new arrow
: an object of that is a new arrow 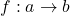 and the diagram assigns the simple extension
and the diagram assigns the simple extension 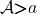 to it, whereas to an arrow
to it, whereas to an arrow 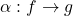 (with
(with 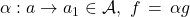 ) it assigns
) it assigns 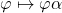 .
.
Now, we get a cocone over 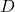 to
to 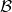 by defining
by defining 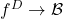 to be the morphism of extensions
to be the morphism of extensions 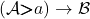 that corresponds to
that corresponds to 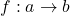 , and actually any cocone over
, and actually any cocone over  , with vertex
, with vertex  determines a morphism of extensions
determines a morphism of extensions 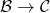 by sending any new arrow
by sending any new arrow 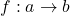 in
in 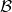 to the image of (the copy of)
to the image of (the copy of) 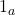 under the corresponding leg map
under the corresponding leg map 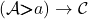 of the cocone.
of the cocone.
![]() (according to Definition 3.) with the category
(according to Definition 3.) with the category ![]() that disjointly contains (isomorphic copies of)
that disjointly contains (isomorphic copies of) ![]() and
and ![]() and for all objects
and for all objects ![]() , the set
, the set ![]() is considered as the homset
is considered as the homset ![]() and its elements are called heteromorphisms. Their compositions with arrows of
and its elements are called heteromorphisms. Their compositions with arrows of ![]() (from the left) and arrows of
(from the left) and arrows of ![]() (from the right) are given by the action of the functor
(from the right) are given by the action of the functor ![]() on the arrows.
on the arrows.![]() where
where ![]() is the category of two objects
is the category of two objects ![]() and a single nonidentity arrow
and a single nonidentity arrow ![]() whose preimage at
whose preimage at ![]() is exactly the collection of all heteromorphisms in
is exactly the collection of all heteromorphisms in ![]() .
.![]() to express that
to express that ![]() is a profunctor from category
is a profunctor from category ![]() to category
to category ![]() .
.![]() and
and ![]() be profunctors
be profunctors ![]() . By a profunctor morphism
. By a profunctor morphism ![]() we simply mean a functor
we simply mean a functor ![]() such that both of its restrictions, to
such that both of its restrictions, to ![]() and to
and to ![]() , are the identity functors.
, are the identity functors.![]() indeed straightly corresponds to a natural transformation
indeed straightly corresponds to a natural transformation ![]() where
where ![]() are
are ![]() .
.
![Rendered by QuickLaTeX.com \[\dia@R=1pc{{\bf 1}\ar[rd]^0 \ar[dd]_a && {\bf 1} \ar[ld]_1 \ar[dd]^b \\ & {\bf 2} & \\ \ct A && \ct B}\]](https://profunctors.zellerede.tk/wp-content/ql-cache/quicklatex.com-09a37fbaad357fb503211e122fd31be8_l3.png)